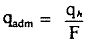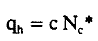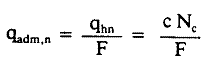En este caso la aplicación de la fórmula general (1), con c =
o, suele dar presiones de hundimiento muy elevadas debido a los grandes valores
de Nq Y NY para los Ø usuales (>30º). Sin embargo, no por ello queda
asegurado que los asientos sean admisibles para las presiones de trabajo así
obtenidas, por lo cual se tiende a fijar dichas presiones en relación con los
asientos.
Dada la dificultad del muestreo y ensayo en laboratorio de estos suelos lo
usual es utilizar parámetros de resistencia o deformabilidad deducidos de
medidas ¡ti situ realizadas con penerrómerros, presiómetros, placas de carga,
etc.
El método más antiguo es el de Terzaghi y Peck (1948) que da las expresiones
siguientes (fig. 2.22):
Fig.
2.22 Asentamientos de zapatas deducidos de la penetración estándar N ( Según Terzaghi
y Peck, 1948)
siendo qadm la presión admisible en Kp/cm2 y s el asiento
tolerable en pulgadas, que en la fig. 2.22 se ha fijado como de 1 pulgada (2,54 cm).
N es el número de golpes medio del ensayo de penetración estándar (S.P.T.) en
la zona de influencia de la cimentación y B el ancho de la misma.
Las expresiones anteriores, que han sido profusamente empleadas, resultan
excesivamente conservadoras por lo que ha habido numerosas propuestas de
modificaciones, aunque aún no existe ningún Otro método universalmente
aceptado.
Posteriormente Meyerhof (1956) recomendó aumentar las presiones admisibles
dadas por Terzaghi y Peck en un 50% y no considerar reducciones en el valor de
N por la presencia del nivel freático, ya que esto quedaba reflejado en el
ensayo. Sin embargo, Schmertmann comprobó que, en el caso de losas o zapatas de
grandes dimensiones, los asientos calculados eran inferiores a los reales.
Bazaraa en 1967 propuso emplear la fórmula

siendo NB = valor N corregido por Ja sobrecarga de tierras a. al nivel de
cimentación según las exprsiones siguientes

y K un factor de corrección obtenido por la relación entre la tensión vertical
a la profundidad B/2 bajo la zapata, en estado seco y la que se produce a la
misma profundidad cuando existe nivel freático.
Schultze y Sherif propusieron en 1973 la correlación que aparece en la fig.
2.23. Los autores señalan que el error de la predicción puede ser de ±40 %. Sin
embargo, se ha comprobado que los errores pueden ser muy importantes en el caso
de cimientos de grandes dimensiones (B > 5 m) y/o cuando el espesor de terreno compresible
es superior a 2B.
Fig 2.23 Correlación propuesta por Schultze y Sherif
Las teorías más recientes tienden a estimar los asientos (y
a partir de ellos la qadm) por integración de deformaciones elásticas,
utilizando correlaciones entre N y el módulo de deformación E. Así, por
ejemplo, en arenas normalmente consolidadas y con niveles de presión medios
(> 1,5 kp/cm2) se obtienen resultados aceptables con los métodos de Webb y
Schmertmann.
Fig
2.24 Método de Schmertmann.
Parry ha sugerido que en arenas flojas (N < 15) y zapatas
superficiales (D/B < 1) de dimensiones moderadas (B <2,20 m) la presión admisible
viene determinada por condiciones de capacidad portante, mientras que en los
demás casos predominan las limitaciones de asientos. Según este autor
resultaría

siendo Nm el valor de N a una profundidad D + 3B/4 bajo la superficie del
terreno.
Para los demás casos propone

siendo s el asiento en cm y B el lado de la zapata en m.
En la fig. 2.25 se han resumido numerosos resultados experimentales expresando,
para diversas compacidades de arena, la relación entre el cociente del asiento
y la presión y el ancho de la cimentación.
Fig.
2.25 Resumen de diversos criterios y
resultados experimentales de asientos de zaptas de arena.
Se ha intentado frecuentemente relacionar los asientos de
placas de ensayo con los de cimentaciones reales. La ley empírica más antigua
es la propuesta por Terzaghi:

que expresa la relación entre el asiento s0 de una placa de 0,30 x 0,30 m2 y el de una cimentación
de ancho B para la misma presión unitaria. La fórmula puede generalizarse para
una placa de lado cualquiera B0:

Como puede verse, para B x, S — 4 so, estableciendo un límite a ¡os posibles
asientos. Sin embargo, las experiencias posteriores han demostrado que tal
límite es improbable y que los asientos aumentan con el tamaño de la
cimentación según leyes de tipo parabólico. En la fig. 2.26 se resumen algunas
de estas recomendaciones.
Fig.
2.26 Relación entre el asentamiento y
las dimensiones de la superficie cargada según datos recogidos de casos reales.